

We shall see that as early as 1676 Leibniz had succeeded in providing a rigorous foundation for Riemannian integration, based on the Archimedean Axiom. “Cum prodiisset” to provide a systematic foundation for his calculus.
#Leibniz infinitesimals series
In section 2 I present this interpretation by tracing its development from Leibniz’s early work on infinite series and quadratures to his unpublished attempt in 1701 in the tract (2008) have argued, this interpretation is no late stratagem, but in place already by 1676. Infinitesimals are fictions in the sense that the terms designating them can be treated as if they refer to entities incomparably smaller than finite quantities, but really stand for variable finite quantities that can be taken as small as desired. Leibniz’s interpretation is (to use the medieval term) syncategorematic: I take the position here (following Ishiguro 1990) that the idea that Leibniz was committed to infinitesimals as actually infinitely small entities is a misreading: his mature interpretation of the calculus was fully in accord with theĪrchimedean Axiom. It has also been read as being at odds with other defences of the calculus Leibniz gave on explicitly Archimedean foundations. It has been construed as a late defensive parry, an attempt to defend the success of his infinitesimal calculus-understood as implicitly committed to the existence of infinitesimals as actually infinitely small entities-in the face of criticisms of the adequacy of its foundations. Leibniz’s doctrine of the fictional nature of infinitesimals has been much misunderstood.
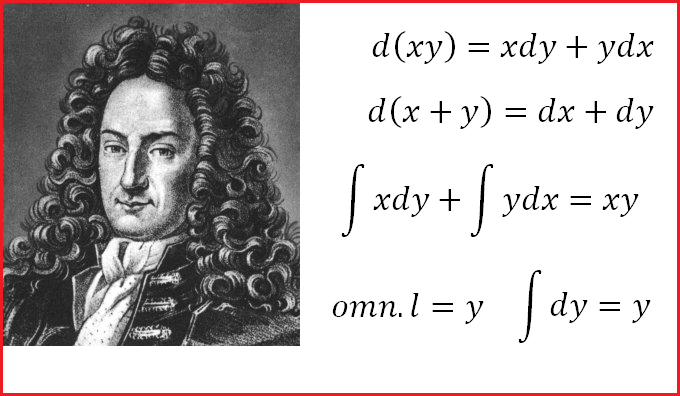
“If the Leibnizian calculus needs a rehabilitation because of too severe treatment by historians in the past half century, as Robinson suggests (1966, 250), I feel that the legitimate grounds for such a rehabilitation are to be found in the Leibnizian theory itself.”- H. Leibniz’s Syncategorematic Infinitesimals R.


I illustrate these differences by a consideration of how each approach might be applied to propositions of Newton’s Principia concerning the derivation of force laws for bodies orbiting in a circle and an ellipse. I find some salient differences, especially with regard to higher-order infinitesimals. I then compare it with the approach of Smooth Infinitesimal Analysis, as propounded by John Bell. In this paper I explain this syncategorematic interpretation, and how Leibniz used it to justify the calculus. In contrast with some recent theories of infinitesimals as non-Archimedean entities, Leibniz’s mature interpretation was fully in accord with the Archimedean Axiom: infinitesimals are fictions, whose treatment as entities incomparably smaller than finite quantities is justifiable wholly in terms of variable finite quantities that can be taken as small as desired, i.e. Arthur Department of Philosophy McMaster University Hamilton, Ontario L8S 4K1 CanadaĮmail: phone: (905) 525-9140, x-23470 fax: (905) 577-0385 LEIBNIZ’S SYNCATEGOREMATIC INFINITESIMALS, SMOOTH INFINITESIMAL ANALYSIS AND SECOND-ORDER DIFFERENTIALS Leibniz's Syncategorematic Infinitesimals, Smooth


 0 kommentar(er)
0 kommentar(er)
